双曲函数模型逆系统控制中大功率放大器的应用

发布日期：2022/12/1来源：网络

实验名称：基于双曲函数的Preisach类迟滞非线性建模与逆控制

实验内容：

压电陶瓷、磁致伸缩等智能材料制备的驱动器件被广泛应用于精密定位领域，但这些智能材料，本身所固有的迟滞非线性严重制约了定位系统的控制精度，并由可能导致系统不稳定。为了减小迟滞非线性对系统的不利影响，通常采用基于迟滞模型的控制方法。

本文基于双曲函数描述Preisach类的迟滞非线性，分别采用2个双曲函数描述迟滞主环的上升段与下降段，并通过坐标变换拟合依附于主环的一阶曲线，然后根据Preisach模型的记忆擦除性与次环一致性原理，用一阶上升曲线描述次环的上升段，一阶下降曲线模拟次环的下降段。基于这种迟滞模型设计了逆控制器来补偿压电双晶片驱动器的迟滞非线性，提高了定位控制的精度。

实验过程：

为了验证双曲函数模型的有效性，设计了逆控制器用于压电双晶片驱动器的精度定位系统，实验系统：装有dSPACE系统的计算机通过功率放大器将驱动电压作用在压电双晶片上，通过光纤位移传感器测量压电双晶片的位移，并将信号传回dSPACE板卡。为了比较控制效果并获得迟滞模型的辨识数据，测量了压电双晶片驱动器在频率为1Hz、50V峰值正弦信号作用下的响应。

响应1.png 响应2.png

控制前：

为了同时测试迟滞主环与次环的控制结果，期望采用1Hz变幅值的正弦信号。

控制前1.png

控制前2.png

控制后：如果迟滞逆模型足够精确，将与压电双晶片驱动器的迟滞非线性相互抵消，使期望位移与响应位移线性化。

控制后1.png

控制后2.png

实验结果：

本文基于双曲函数描述Preisach类的迟滞非线性，分别采用2个双曲函数描述迟滞主环的上升段与下降段，并通过变换坐标拟合了依附于主环的一阶上升与下降曲线，然后根据记忆擦除性与次环一致性描述迟滞非线性的任意次环。这种建模方法所需的模型参数远小于经典的Preisach模型，而且参数识别容易，使用该模型的前提是双曲函数能够拟合迟滞非线性的主环，这适用于控制压电驱动器等智能材料的迟滞非线性。基于该迟滞模型设计了压电双晶片驱动器的逆控制器，使控制后的最大定位误差比控制前减小了44.26%，可有效抑制迟滞非线性引起的误差。

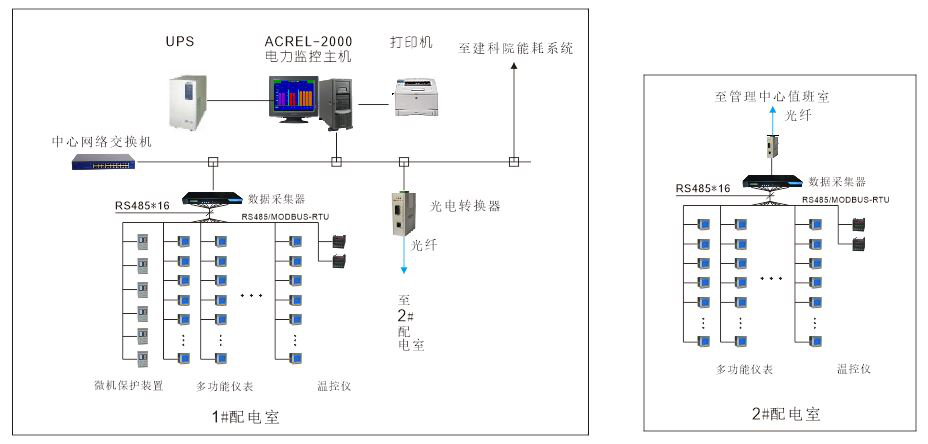欧美金融城电力监控系统的设计与应用 1 项目简介：欧美金融城是杭州未来科技城CBD核心区的规划金融港，东至闲林港西路、南至红卫北路、西至规划道路、北至规划道路，整体规划建筑面积近百万平方米，涵盖地铁上盖都市美式住宅、超甲LEED白金写
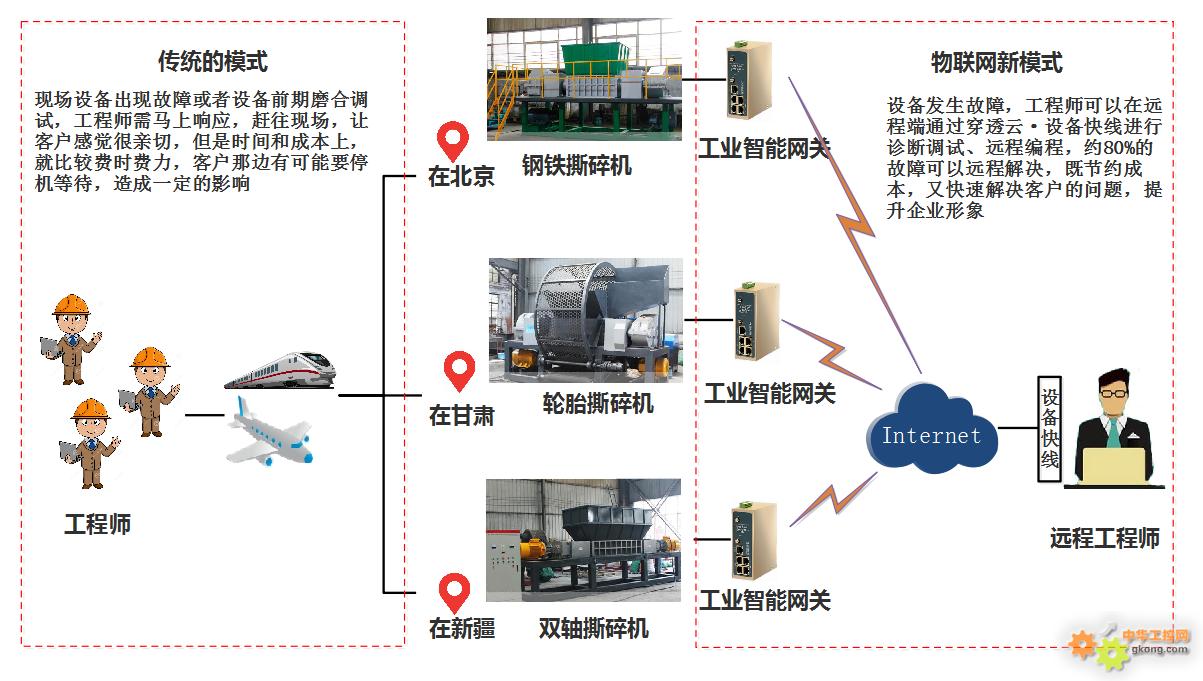垃圾处理设备远程调试远程运维系统项目背景垃圾处理设备主要项目包括：生活垃圾破碎分选系统、大件垃圾资源化处理系统等,产品分布较广，环境恶劣.其希望能对分布各在世界地的项目集中数据监控管理、远程调试、远程运维等，通过监控画面观察周边环
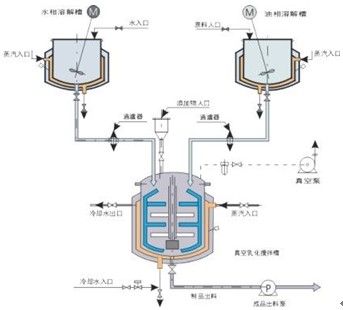台达PLC在乳化机控制系统中的应用 1 序言真空均质乳化机（简称乳化机）主要应用于化工、医药、生物、食品等诸多领域中非均相液一固和液一液多相体分散体系的混合。目前该设备在国内主要是采用传统的继电器控制系统构成，操作人员需要根据经验
电力配网远程监控系统解决方案　　一、项目背景　　电网建设繁杂庞大，时间跨度大，各种新老设备混于其中，很多电网架构已经不是有当今社会发展的需求，但是电网改造成本巨大，不是一朝一夕的事情。如若遇到自然灾害等其他一些未知的破坏等事故
变电站智能辅助监控系统解决方案传统的变电站安防智能化系统受传统理念和技术的影响，各个子系统都是孤立的，以至于出现丁一种监控孤岛现象，无形中降低了系统的实用性、稳定性和安全性，而且增加了投资成本。尤其是现在变电站系统平常的生产过
苏州漕湖邻里中心电能管理系统的设计与应用赵斌11安科瑞电气股份有限公司，上海嘉定201801；摘要：介绍苏州漕湖邻里中心电能管理系统，采用智能电力仪表采集配电现场的各种电参量和开关信号。系统采用现场就地组网的方式，组网后通过现场总线通讯并远
光伏电站电力监控装置及系统-安科瑞郭海霞安科瑞郭海霞　　江苏安科瑞电器制造有限公司江苏江阴 214405　　1、概述　　太阳能光伏电站主要由光伏电池阵列、汇流箱、低压直流柜、逆变柜、交流低压柜、升压变压器等组成，最后产生的交流直接并入
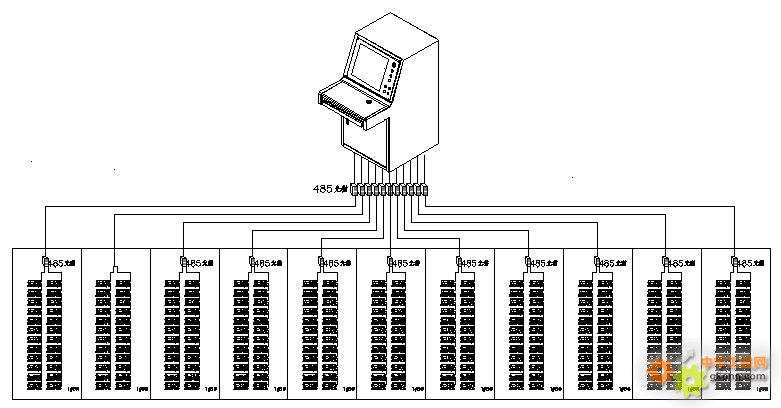Acrel-6000电气火灾监控系统在熙璟城项目的应用赵斌安科瑞电气股份有限公司上海嘉定【关键词】：火灾探测器；电气火灾；商业住宅；1、项目简介熙璟城总建筑面积30万㎡，由12座30-32层高层住宅、1座3层十二班幼儿园围合而成。住宅总计1591户，设